This blog, and series, will be a way more difficult story to tell than I'd thought it would be.
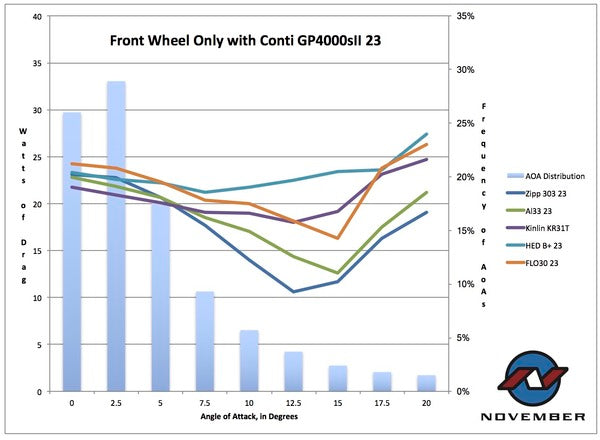
What we'd expected was that the Zipp 303 reference wheel would be that shade faster at the heavily prevalent and thus more important narrow angles of attack (aka yaw angles), and then extend that lead out into the angles that occur with much less frequency. What actually happened was that the Al33 (our RFSW3 wheelset's rim) and the Kinlin XR31T (that we use in the FSW3) both performed better than the 303 at the most prevalent low yaw angles, starting to cede a bit at around 7.5* and going on from there.
When you do a test like this, you get a lot of data, and it takes a while to chew and digest it. What we present here is just a first, very broad, pass at things.
The blue vertical bars that you see in the graph are the amount of time the average cyclist is likely to spend encountering each wind angle during a ride. We will offer a very complete explanation of that in the next blog.
For now, we're just trying to wrap our heads around this, and make good on all the teasing that we've done. Sorry for that, hope it was worth it.
Enjoy

20 comments
Hi Joe,Simple answers all around. We didn't compare it to a 34 because the 34 isn't available anymore, so it's an irrelevant comparison. It's also not that well known. We didn't choose a 202 to compare it to, because no one thinks of a 202 as a fast aero wheel. So we thought that people would think "who really cares how your aerodynamics compare against a wheel that no one considers for its aerodynamics?" Dave
I am very pleased with the information in this article, note 10!Good article! Very nice!
You guys are the fucking best. And you continue to set the standard for general wheel tech bloggage content. Thanks.-J
It seems a big part of interpreting these results is how it's determined what the distribution of yaw angles are. What kind of speeds are these for, what locations, etc…information on the sampling to determine the distribution of yaw angles. If it's for a high speed, it'll skew the distribution to lower yaw angles. Also, if this is for a given windspeed at that given yaw angle, which means that the actual headon windspeed will be lower as the yaw angle increases? How much of the "reduced" drag is due to the headon windspeed being lower (as a result of coming from the side) vs the aerodynamics of the wheel?Ironically, it seems a slower rider, who will experience a higher distribution in the higher yaw angles, will actually benefit from the Zipps? Obviously that's offset by the fact that slower speeds have exponentially less aero drag.
Hi Chris – Sorry I missed this comment. Most of your questions are addressed in the next post, and to get the complete story you have to read the source material behind the wind distributions. Decide for yourself what's relevant to you once you've taken all that onboard. Slower riders are more likely to experience wider angles, you are correct, but air resistance increases/decreases exponentially so when you slow down, air resistance becomes a lesser part of your total drag package.