One of the chief aims of the Rail series was to provide a stable and manageable ride. This was a major consideration in the 52 being the 52, and not the 58 or the 60 or the 62. The 34 was in large part born from the market demand for a wheel that would be nigh on invisible to crosswinds, even though early 52 reviews were near unanimously positive in regard to manageability.
The cross sectional design of Rails attempts to create a near symmetry between rim side and tire side. Obviously, tire choice affects this. We had a 23 in mind, aware of the size to which most 23s would inflate on our chosen 18mm bead seat width. Different tires have different shapes, and many people use different sizes. Nonetheless, the general gist stands.
To date, crosswind stability has been measured subjectively and anecdotally, never directly measured and quantified. Thankfully, a wheel company from Indiana had been pestering A2 for an actual measured match to their CFD predictions. Recently, A2 completed the measurement apparatus and algorithms to provide these measures. When you test a wheel now, your data sets include two new columns - coefficient of drag, and center of pressure.
Ceofficient of drag, simply stated, is how much pressure is pushing against your wheel - how strong is the push. Units of measure are non-specific, but linear - meaning that .20 is twice as hard a push as .10, and 2/3 as big a push as .30. Center of pressure describes the position of the push, relative to the hub, measured in centimeters. Center of pressure of 2.35 would describe a push centered 2.35cm in front of the hub. -3 would describe a push 3cm behind the hub.
To date, we've never seen any graphical presentation of this data. It's too new a concept, so we've taken a stab at it, which we think provides a clear picture of the relative power and placement of the crosswind's push on each wheel. We have once again used the Tour Magazine angle of attack weighting in creating this chart, but we have used the 25mph weighting. Our reasoning for this is that as wind speeds increase relative to bike speed, the likelihood of wider angles of attack increases. We expect and welcome questions about this information and presentation, simply because we want it to be easily understood.
Here is a link to a page that allows you to calculate apparent wind speeds and angles for any given combination (be sure and use the second box, the first one calculates to true wind speed). Be aware as you do this that a windy city will have an average windspeed of somewhere around 10mph (the calculator uses knots - 10mph equals 8.7 knots), as measured at that city's airport. Airport windspeed is measured high off the ground in an unobstructed place, and will overstate what your wheels are riding in by quite a bit - like 50% or more.

To say the results pleased us would be an understatement. As the initial test of the 34 was underway, I was busily prepping the next wheel to test in the work room and poked my head into the control room to ask if I was in a good mood. Dave, A2's engineer and a man not given to subjective statements or value judgments, said the aero drag measurements were going right along, but that the pressure measurements should put me in a very good mood indeed. As the 52 ran and the data came up, my mood improved even more.
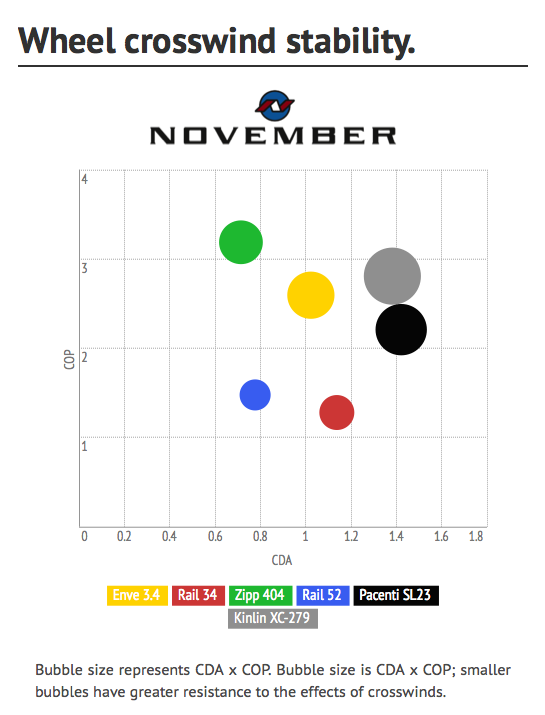
As you can imagine, we're excited to see that our consideration of crosswind stability in the design of the Rail has been confirmed with such excellent results.

16 comments
All, The CdA is the magnitude of the push, the CoP is the placement of it. Think of this whole thing as "foot pounds" that is measured on a horizontal line going through the wheel's hub. CoP is the "foot" part (how long is the lever of the push), CdA is the "pounds" part (how hard is the push at the end of that lever). It is a difficult thing to describe verbally or graphically, but the foot pounds analogy should work. 2 pounds at 1 foot and 1 pound at 2 feet yield the same number of foot pounds, and that is the same deal here. We know we had one factor (steering axis) that will change the relative ordering of the wheels (discussed above – alloys get much better), and we will post a new chart reflecting that. Dave
Dave,Your post, above, seems to suggest that the CdA is force, but you speak elsewhere as if it is pressure (force/area). Can you clarify, as it makes a big difference? (Given the same pressure, a larger area will result in greater force.)
Peter, It is stated as pressure (m^2), but A2 describes it more like force. It's a bit of a black box formula (they protect their IP), but when I asked for it to be broken down in the simplest terms to be properly expressed, it was stated as "CdA shows how hard the push is, CoP shows where it happens."Let me describe it this way, and then I have to build wheels all day. On a sailboat, you have underwater lifting surfaces and the sails are above the water. The net location of the "balance point" among the underwater surfaces is the center of lateral resistance. The net location of the center of effort of the sails is called, simply enough, the center of effort. In order for the boat to track in a straight line with no rudder input (you can sail a boat without a rudder, even), you must align the center of effort directly over the center of lateral resistance. If the CoE is forward of the CLR, the boat will turn away from the wind. If the CoE is behind the CLR, the boat will turn into the wind. The size of the sails will determine how much the boat heels over, but does not directly determine whether the boat will steer in a straight line. In this measurement, A2 is giving you the answer to the "will the boat steer straight, turn into the wind, or turn away from the wind" answer. It is not telling you how much you heel over. I hope that does it because that's about as well as I can explain it. Dave
Dave,Thanks: this is helpful. I do think that the issue of pressure vs. force is a big one. If you need to multiply CdA by reference area (basically the cross section of the rim+tire+hub) to get force, much of the advantage of the Rail 52 disappears.
Those values are in m^2, they are the final values.